Pseudocode
After this lesson you should be able to:
Like the last lesson this lesson is quite large but as you learn more the course gets easier! The major differences between this lesson and the previous are:
This lesson and the next lessons two use pseudocode to introduce quite a few topics. Keep in mind though that most of the topics can be applied to the other methods of stating algorithms.
There is an exercise for you to do, the exercise has a sample answer: Exercise 1: a first design using pseudocode
When you have finished the lesson you might like to attempt these questions to assess how much you have learned.
Pseudocode, like step-form, is a written way of stating algorithms but uses a much more restricted vocabulary. It is very much like a 3GL and for many programmers and program designers is the preferred way to state algorithms and program specifications.
Although there is no standard for pseudocode it is generally quite easy to read and use, for instance here is some pseudocode:
As you can see it is a precise statement of a while loop.
Pseudocode is a written statement of an algorithm using a restricted and well-defined vocabulary. In the next section you look at the vocabulary in detail.
It is useful to separate the pseudocode into several groups as shown here:
| Group | Key words | Example |
| Input/Output | INPUT, READ
Used to get values from a data source, a keyboard for instance DISPLAY
|
INPUT counter
DISPLAY new_value |
| Iteration | REPEAT
statement UNTIL <condition> The Repeat ... Until loop which was introduced in the introductory lesson on algorithms. The REPEAT loop executes the statement until the condition becomes true. DOWHILE <condition>statement END DOWHILE This is the While loop also introduced in the introductory lesson on algorithms. The WHILE loop executes the statement while the <condition> is true. FOR <var> = <start value> to <stop value>
You haven't seen this loop before but it is a special case of the While loop. The FOR loop iterates for a fixed number of steps. The While and Repeat loops can be for a variable number of steps. |
SET count_value TO 0
REPEAT DISPLAY count_value ADD 1 TO count_value; UNTIL count_value > 10 DOWHILE count_value < 10
FOR count = 1 to 10
The statements inside the loops are indented to aid the readability of the pseudocode. |
| Decision |
IF <condition> THEN
statement ENDIF IF <condition>
Both of these decision forms were first introduced in the algorithms introductory lesson. |
IF count > 10
THEN DISPLAY count ENDIF IF count > 10
|
| Processing | ADD, SUBTRACT, COMPUTE,
SET |
ADD 3 TO count
SUBTRACT 5 FROM count SET count TO 12 COMPUTE 10 + count GIVING new_count |
Although the processing group are very useful most program designers tend to prefer to use operators like:
These are the arithmetic operators.
These are more intuitive since we use them in arithmetical expressions and they are easier to write, for instance:
The assignment operator, = (as count = count + 32) means assign the results of the operation on the right-hand side to the variable on the left-hand side.
There are two other classes of operators which are useful in psuedocode. One class is called the relational operators. These are used to evaluate the relationship between variables and are:
Here are some examples of the use of the relational operators:
| IF count == 32 THEN ... | This decision states that if the variable count contains 32 execute the statement following THEN. |
| DOWHILE count <= 50
... END DOWHILE |
The statements in the while loop will execute while the value of count is 50 or less. |
| REPEAT
... UNTIL count > 12 |
The statements in the repeat loop will execute until the value of count exceeds 12. |
| IF count <> total THEN ... | If the value of count is not the same as the value of total execute the statement following THEN. |
Don't confuse == (equal) with = (assignment). The first determines if a variable is the same as a value or another variable, but the second (assignment) makes a variable become some value. Remember == is two equals signs.
A statement like count <= 50 is a proposition, you might remember from an earlier lesson that a proposition is a statement that has a truth value, it can be TRUE or FALSE. If count is less than or equal to 50 then the proposition count <= 50 is true. For example some pseudocode might help:
count = 51
IF count <= 50 THEN DISPLAY 'Count is less than 51' ENDIF
IF count > 50 THEN DISPLAY 'Count is greater than 50' ENDIF
The other class is called the logical operators which are used to form compound propositions and the logical operators are:
| AND | IF (x = = 32) AND (y = = 7) THEN sumxy = x + y |
| OR | IF (letter = = 'A') OR (letter = = 'E') THEN DISPLAY 'Vowel' |
| NOT | IF NOT (letter = = 'A') THEN DISPLAY 'Not letter A' |
The logical operators can be used to combine relational expressions.
The statement IF (x == 32) AND (y == 7) THEN sumxy = x + y says that if it is true that x == 32 AND it is also true that y == 7 then add x and y together and store the result in variable sumxy.
The statement IF (letter == 'A') OR (letter == 'E') THEN DISPLAY 'Vowel' says that if the variable letter contains either 'A' or 'B' then display the word vowel on the output device. The whole expression (letter == 'A') OR (letter == 'E') is false if both letter == 'A' is false and letter == 'E' is false.
The NOT operator in the last example statement IF NOT (letter = 'A') THEN DISPLAY 'Not letter A' is used to reverse the sense of a relational expression. If it is true that letter is equal to 'A', the NOT operator in NOT (letter = 'A') will give a value of FALSE.
| Expression | Result |
| A >= 20 | TRUE |
| A > 20 | FALSE |
| A == B | FALSE |
| A == B + 5 | TRUE |
| (A > B) AND (A > 20) | FALSE |
| (A > B) OR (B > A) | TRUE |
| (A < B) OR (B > A) | FALSE |
| NOT (A > B) | FALSE |
| NOT (NOT (A > B)) | TRUE |
What do we do with an expression like x = a * b + 7? If a is 10 and b is 5 is the answer 57 or is it 120? In other words do we do the multiplication part first (a * b) followed by the addition ( + 7) or do we do the addition part first (b + 7) then multiply by a?
You might remember from school that there is an order of precedence for evaluating arithmetic expressions. In my day it was called PODMAS or BODMAS which I think meant parentheses (or brackets) outside divide, multiply, add, subtract. This means do what inside the parentheses first, and do divide, multiply before add and subtract. If we apply the PODMAS rule in the case of x = a * b + 7 the correct answer is 57.
The same applies in computer languages and for our operators, arithmetic, logical and relational the order of precedence is:
The precedence is from top to bottom and on each line from left to right. Evaluate whatever is in parentheses first, then NOT followed by *, /, AND then +, -, OR then last the relational operators.
Probably the best way to start with pseudocode is to see an example so I've copied the vowel-counting sample from an earlier lesson and re-written it using pseudocode:
|
curr = 1
last = 6 count = 0 REPEAT READ letter IF letter is vowel THEN count = count + 1 curr = curr + 1 UNTIL curr > last |
Like the step-form the pseudocode executes from the first statement at the top down to left obeying any branching statements that might occur in decisions and loops.
Whenever you are acquiring new skills there is no substitute for practice but first I will show you another example.
The problem: Design a program which accepts as input two numbers in the range 0 to 99 inclusive and which sums the numbers, finds the difference of the numbers and displays both the sum and the difference.
We have some processes:
and perhaps not so obvious,
We have some variables:
We have some decisions:
There are no loops that I can see so it's time to build a preliminary algorithm.
Here is a first effort:
| INPUT Number_1
INPUT Number_2 Sum = Number_1 + Number_2 Difference = Number_1 - Number_2 DISPLAY Sum DISPLAY Difference |
The first stab is OK except that I haven't checked to make sure the numbers are in the correct range. My next attempt is one way I could do that. |
| 1 REPEAT
2 INPUT Number_1 3 UNTIL (Number_1 >= 0) AND (Number_1 <= 99) 4 REPEAT
7 Sum = Number_1 + Number_2
|
You can see that I was wrong about there being no loops in the algorithm. I've used repeat loops that will ensure that Number_1 and Number-2 are in the correct range. In the case of Number_1 the loop will not terminate until it is true that Number_1 is greater than or equal to 0 AND it is true that Number_1 is less than or equal to 99. The numbers next to the statements are just for the trace table which follows. |
I have abbreviated variable names to minimise the column widths:
| Step | N1 | N2 | Sum | Diff | N1 >= 0 | N1 <= 99 | N1 >= 0 AND
N1<= 99 |
N2 >= 0 | N2 <= 99 | N2 >= 0 AND
N2 <= 99 |
| 1,2,3 | -1 | ? | ? | ? | FALSE | TRUE | FALSE | ? | ? | ? |
| 1,2,3 | 102 | ? | ? | ? | TRUE | FALSE | FALSE | ? | ? | ? |
| 1,2,3 | 10 | ? | ? | ? | TRUE | TRUE | TRUE | ? | ? | ? |
| 4,5,6 | 10 | 6 | ? | ? | TRUE | TRUE | TRUE | TRUE | TRUE | TRUE |
| 7 | 10 | 6 | 16 | ? | TRUE | TRUE | TRUE | TRUE | TRUE | TRUE |
| 8 | 10 | 6 | 16 | 6 | TRUE | TRUE | TRUE | TRUE | TRUE | TRUE |
In the first two lines of the trace table you can see that since the values of Number_1 are outside the range the expression (Number_1 >= 0) AND (Number_1 <= 99) evaluates to FALSE. This means that the algorithm stays in the repeat loop.
It's now time for you to do some of your own work.
All measurements should be in metres.
I have given a sample answer here but as with the other exercises try to work it out for yourself first.
The last topic in this lesson on pseudocode deals with an important concept in program design - the concept of the subprocess. Subprocesses are also known as subroutines, subprograms, procedures and functions. The topic isn't essential to your understanding of pseudocode and you might decide to skip it for now. However it will be very useful to read this if you are planning to go on to do some programming.
The subprocess is important for a number of reasons, amongst these are:
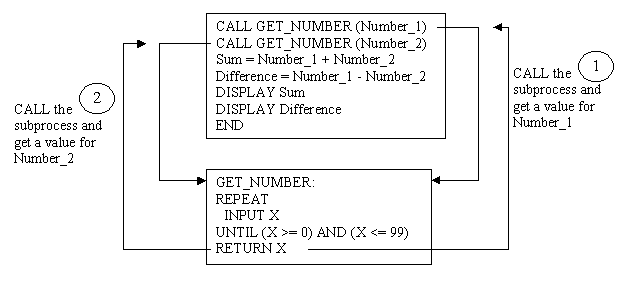
In pseudocode we can write a process and give it a name, for example:
You will recognise this as the first repeat loop from Pseudocode algorithm example 1 except that I've added a couple of things. I've named the repeat loop GET_NUMBER: and I've added a new pseudocode statement RETURN.
It might help you to understand it if I first use it then I explain it.
| CALL GET_NUMBER (Number_1)
CALL GET_NUMBER (Number_2) Sum = Number_1 + Number_2 Difference = Number_1 - Number_2 DISPLAY Sum DISPLAY Difference END GET_NUMBER:
|
The CALL statement is another new pseudocode statement. It directs the algorithm to find a subprocess called GET_NUMBER and execute it. The CALL statement also passes a parameter in parentheses (Number_1 or Number_2) to the subprocess. In effect CALL transfers the sequence to the subprocess. When the subprocess finishes it has a RETURN statement which returns to the main program to the statement following the original CALL. The RETURN statement also returns a value for the parameter. In this example the first CALL has Number_1 as a parameter and the subprocess returns whatever value X had which becomes Number_1. The second CALL has Number_2 as a parameter and the subprocess returns whatever value X had which now becomes Number_2. The END statement at the end of the main program separates the main program from the subprocess or subprocesses if there happens to be more than one. |
 |
You will probably agree that this has been quite a substantial lesson but you should have learned a great deal, not just about pseudocode but also about topics that are very relevant to computer programming. If you go on to learn computer programming you will find that the skills learned here will have a very practical application to the task of learning a computer language.
In this lesson you studied:
Although there was a lot of material you don't have to digest it all at once, you can come back and review it. Remember also that as the course continues most of the things you learn are reinforced in new ways as you cover the material that follows.
Return to the index
Go to the next lesson
Return to the previous lesson
This publication is copyright David Beech and Learning Systems 1997-2002
and may not be reproduced by any means without the written permission of
David Beech.
9 Wyndella Street, Tasmania, Australia